Malayalam language, spoken predominantly in the south Indian state of Kerala has an alphasyllabary writing system. Like other Brahmic scripts, the consonant-vowel sequences is written as a single unit- the consonant letter being the base and the vowel notation secondary. The u and uː vowel signs of Malayalam modifies the shape of the associated base consonants (or consonant clusters, called conjuncts). This article discusses various ways in which the shape of consonants get modified when followed by the vowel signs, u and uː.
The orthographic script style of Malayalam was reformed or simplified in the year 1971 by this government order. A detailed analysis of its reasons and its impact on popular culture is available here. The reformed orthography is what is taught in schools. The textbook content is also in the reformed style. The prevailing academic situation does not facilitate the students to learn the exhaustive and rich orthographic set of Malayalam script. At the same time they observe a lot of wall writings, graffiti, billboards and handwritings that follow the exhaustive orthographic set.
The sign marks for the vowels ഉ and ഊ (u and uː) have many diverse forms in the exhaustive orthographic set when joined with different consonants. But in the reformed style, they are always detached from the base consonant with a unique form as ു and ൂ respectively for the vowel sounds u and uː. Many native Malayalam speakers learn to read both of these orthographic variants either from school or from everyday observations. But while writing the styles, they often get mixed up as seen below.
The green mark indicates the usage of reformed orthography to write പു (pu), blue indicates the usage of exhaustive set orthography to write ക്കു (kku). But the one in red is an unusual usage of exhaustive orthography to write ത്തു (ththu). Such usages are commonplace now, mainly due to the lack of academic training as I see it.
In this blog post, I try to consolidate the vowel signs of u and uː referring to early script learning resources for Malayalam.
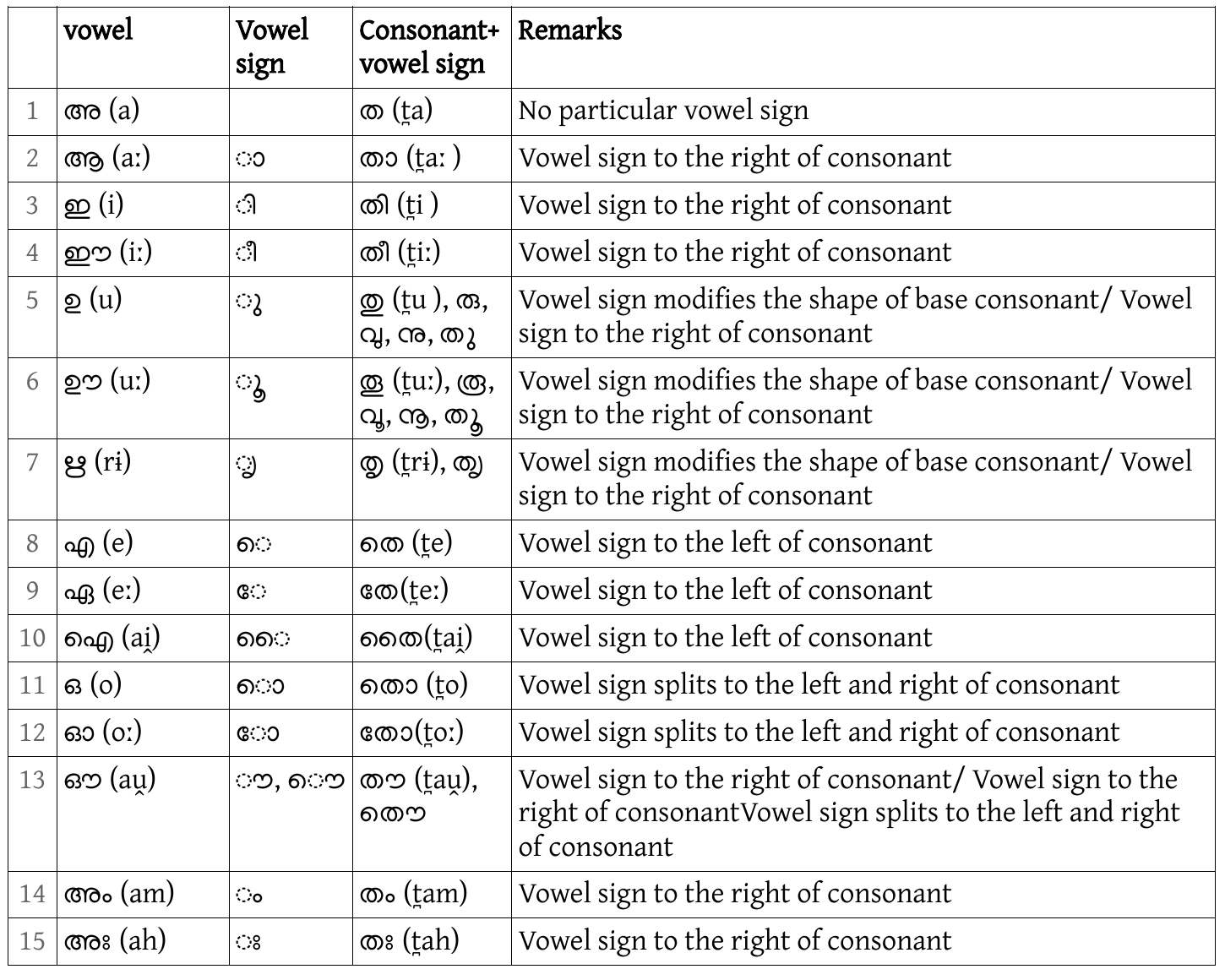
Vowel signs in Malayalam
Vowels have independent existence only at word beginnings. Otherwise, they appear as consonant sound modifiers, in form of vowel signs. These signs often modify the glyph shape of consonants and this is a reason for the complex nature of Malayalam script. These marks can get distributed over the left and right of the base consonant. See the table below:
As seen in the table, the signs ു [u], ൂ[uː], ൃ [rɨ] changes the shape of the base consonant grapheme. You can see the detached form as well in rows 5,6 and 7 of the above table.
How does the vowel sign for ‘ു’ [u] and ‘ൂ’ [uː] affect the base consonant?
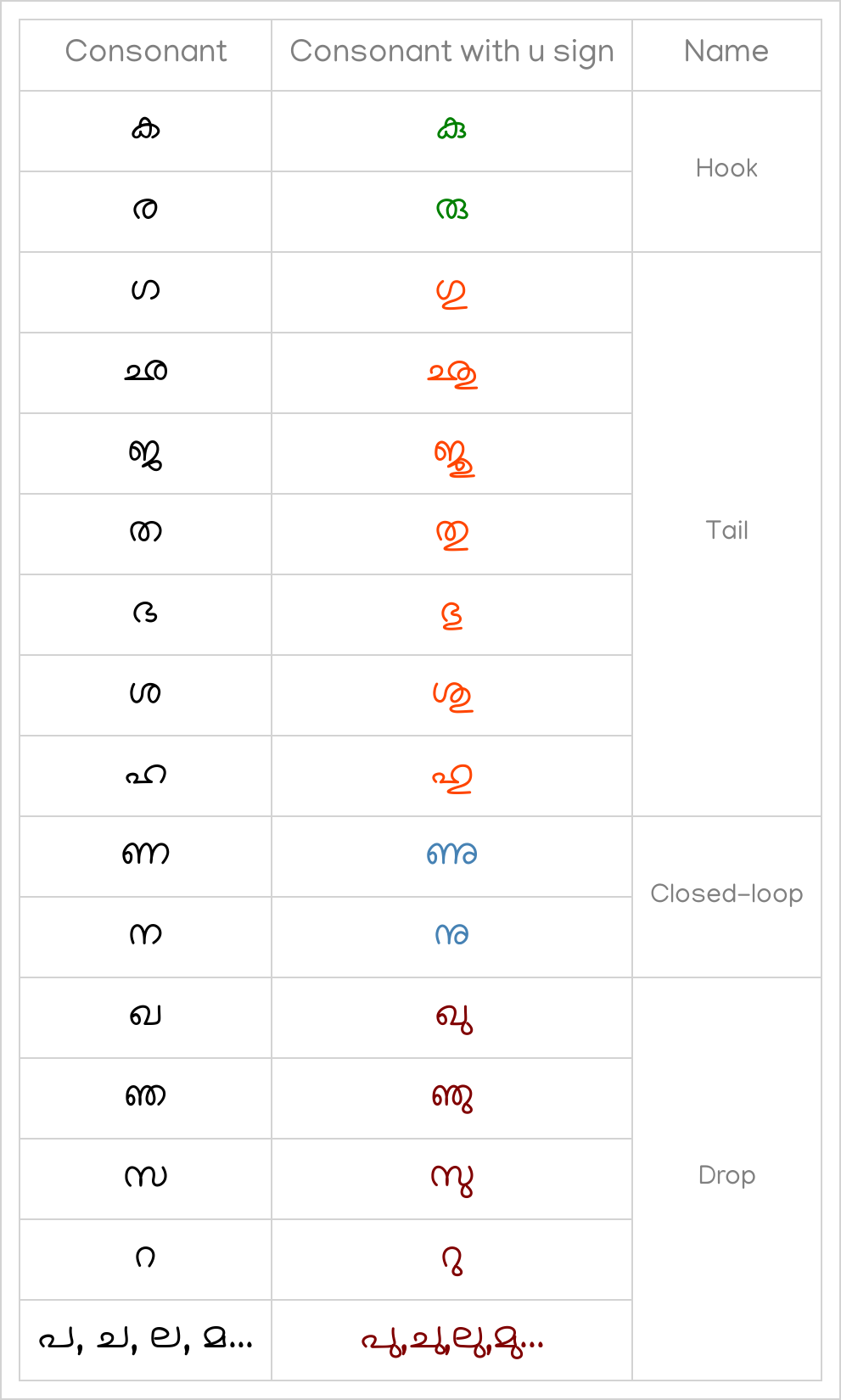
In the exhaustive script set of Malayalam, there are in fact 8 ways in which ‘ു’ [u] and ‘ൂ’ [uː] signs change the shape of base consonant grapheme. These 8 forms (4 forms of u and 4 forms of uː ) are consolidated below. The four different shapes are named as in the final column.
From the table,- ക(ka), ര(ra) gets modified by a shape we hereby call as hook. The same shape change applies to all conjuncts that end with ക as in ങ്ക(n̄ka), ക്ക(kka), സ്ക(ska) and സ്ക്ക(skka). As the conjuncts that end with ര(ra) assumes a special shape the hook-shaped sign does not apply to them.
- ഗ(ga), ഛ(ʧʰa), ജ(ʤa), ത(t̪a), ഭ(bʱa), ശ(ʃa), ഹ(ɦa) gets modified by a shape that resembles a tail that comes back to right after moving left. Those conjuncts which end with these consonants also assume the same tail shape when ‘ു’ [u] vowel sign appear after them.
- ണ(ɳa) and ന(na/n̪a) changes their shape with an inward closed loop. Those conjuncts which end with these consonants also assume the same loop shape when ‘ു’ [u] vowel sign appear after them. For example ണ്ണ(ɳɳa), ന്ന(nna), ക്ന(kna) etc.
- All other consonants use the drop shape. As it is the most popular among all [u] signs, it is often mistakenly used instead of the other signs mentioned above. This case is indicated in the red circle in the figure captioned u sign forms on wall writings.
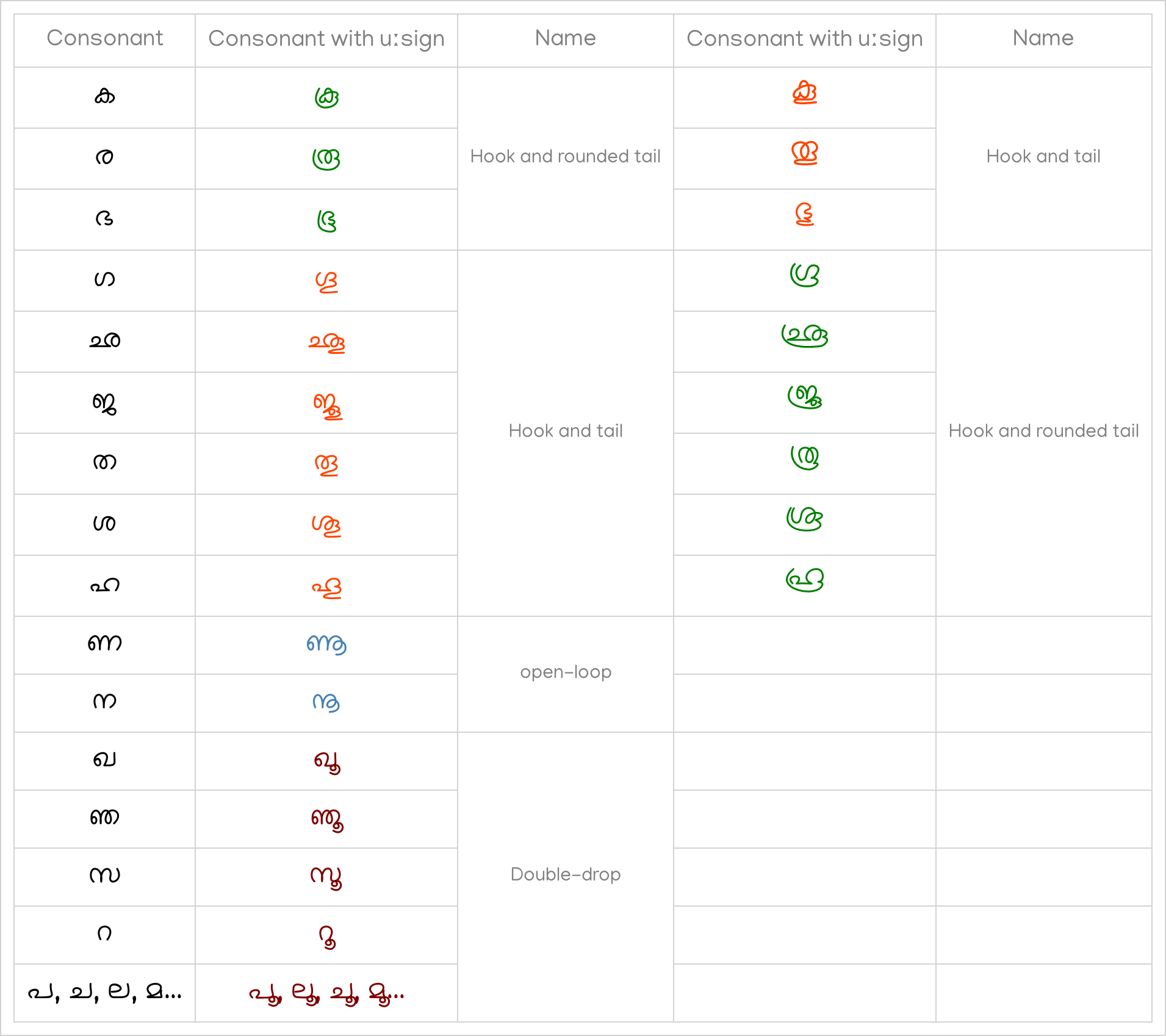
- ക(ka) , ര(ra), ഗ(ga), ഛ(ʧʰa), ജ(ʤa), ത(t̪a), ഭ(bʱa), ശ(ʃa), ഹ(ɦa) can have two alternate uː sign forms. The first shape is hook and tail shape while the second one is hook and rounded tail.
- Hook and rounded tail is more popular with the consonants ക(ka) , ര(ra) and ഭ(bʱa)
- Hook and tail is more popular with the consonants ഗ(ga), ഛ(ʧʰa), ജ(ʤa), ത(t̪a), ശ(ʃa) and ഹ(ɦa)
- The outward open-loop shape is assumed by the ‘ൂ’ [uː] sign mark when associated with the consonants ണ(ɳa) and ന(na/n̪a)
- All other consonants use the double-drop shape. As it is the most popular among all [u] signs, it is often mistakenly used instead of the other signs mentioned above.
Note: The sign shape names drop, double-drop, hook, hook and tail, hook and rounded tail, tail, closed loop and open loop are the author’s own choice. Hence there are no citations to any literature.
Early texts on Malayalam script and orthography
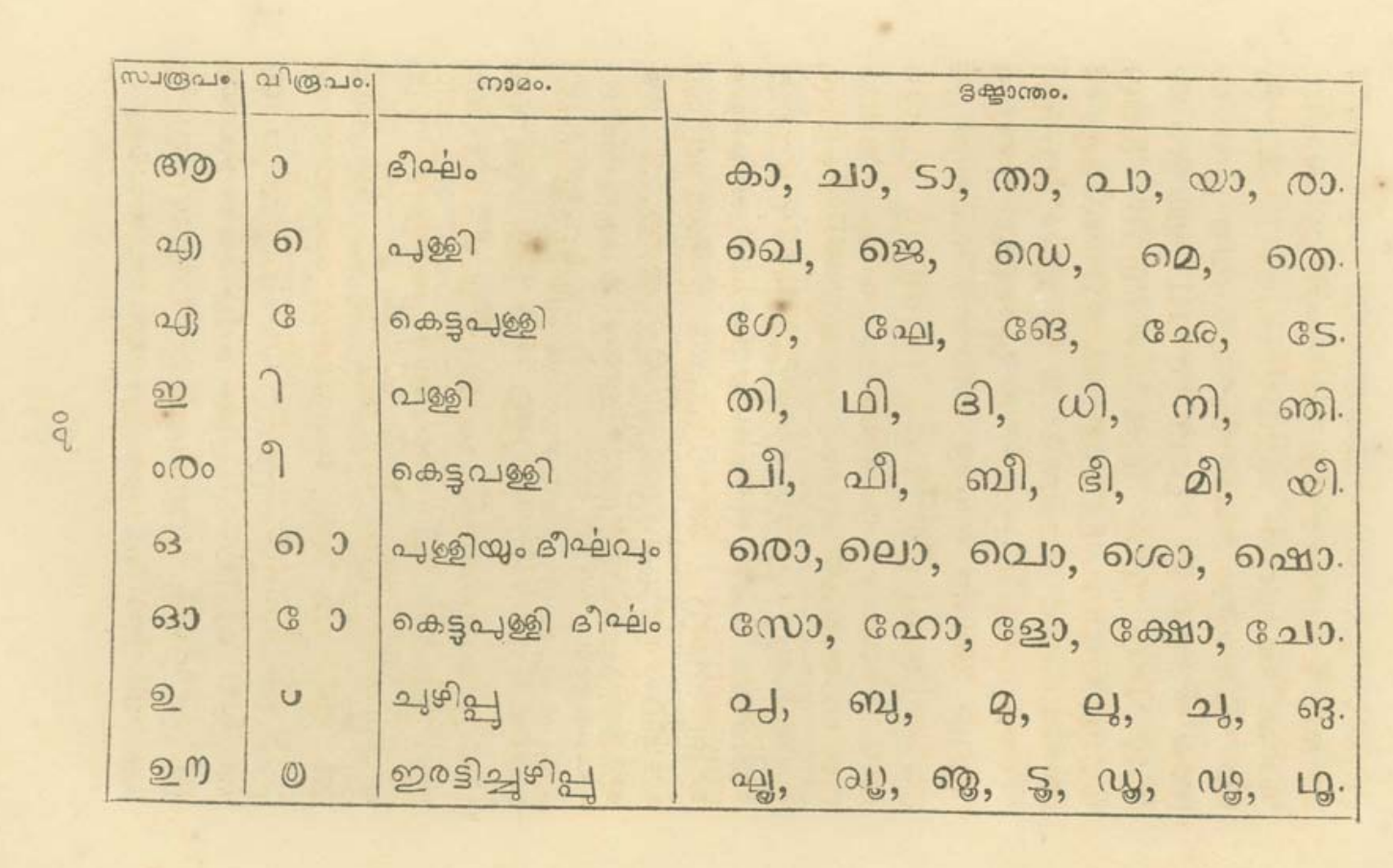
Modern Malayalam textbooks do not detail the ‘ു’ [u] and ‘ൂ’ [uː] vowel sign forms. The earliest available reference to the script of Malayalam and its usage is the book from 1772, Alphabetum grandonico-malabaricum sive samscrudonicum. It was a textbook meant to be used by western missionaries to Kerala to learn the Malayalam script and its language of description is Latin. Alphabetum describes various vowel sign forms but it does not give any indication on the hook and tail form. ക(ka), ര(ra), ഗ(ga), ഛ(ʧʰa), ജ(ʤa), ത(t̪a), ഭ(bʱa), ശ(ʃa), ഹ(ɦa) etc. uses the hook and rounded tail form only. This being the first-ever compilation of Malayalam script usage, that too by a non-native linguist, there are chances for unintended omissions about which I am not sure of. The metal types used in this book were movable and were the first of their kind to be used to print a Malayalam book. The same types were used to print the first-ever complete book in Malayalam script- Samkshepavedartham.

‘Excerpt from Alphabetum grandonico-malabaricum sive samscrudonicum describing the usage of ‘ു’ [u] and ‘ൂ’ [uː] signs
He clearly mentions the two alternate forms of hook and tail as well as hook and rounded tail in his book on the Grammar of Malayalam.
Contemporary usage of orthographic styles
The early attempts to describe the script of Malayalam with all its complexity is seen in these books in the initial days of the printing era. Much later, in 1971 reformed script orthography was introduced to the language and culture aiming at overcoming the technological limitation of Malayalam typewriters. But the language users never abandoned the then-existing style variants. Now we see around us a mix of all these styles.
Note: This post was originally written in Malayalam. Use this link if you would like to read the original.